Abstract

We present the Neural Physics Engine (NPE), a framework for learning simulators of intuitive physics that naturally generalize across variable object count and different scene configurations. We propose a factorization of a physical scene into composable object-based representations and a neural network architecture whose compositional structure factorizes object dynamics into pairwise interactions. Like a symbolic physics engine, the NPE is endowed with generic notions of objects and their interactions; realized as a neural network, it can be trained via stochastic gradient descent to adapt to specific object properties and dynamics of different worlds. We evaluate the efficacy of our approach on simple rigid body dynamics in two-dimensional worlds. By comparing to less structured architectures, we show that the NPE's compositional representation of the structure in physical interactions improves its ability to predict movement, generalize across variable object count and different scene configurations, and infer latent properties of objects such as mass.

You can read the full paper here, view the poster here, and watch the spotlight presentation here.

Model

By design, the NPE scales to scenes with a large variable number of objects. It models a particular object's velocity (object 3 in this case) at t + 1 as a composition of the pairwise interactions between itself and other neighboring context objects during t and t - 1. Further details are in the paper.

Results

Below we present results that show the NPE's efficacy in prediction, generalization, and inference. For the predictions below, the model is provided with two timesteps as input and predicts all subsequent timesteps with no external supervision. Concretely, the NPE takes two previous timesteps as input and predicts the velocity of each object for the next timestep. This predicted velocity is used to update the objects' positions, which become part of the input for the next prediction.

Because these physical systems are chaotic systems, it is not surprising that the model predictions diverge from the ground truth after a couple of seconds. However, note that the NPE learns physical concepts such as solidity of objects, inertia, and collisions that continue to be preserved throughout these rollouts. Crucially, this knowledge can be transferred and extrapolated to worlds with a number of objects and object configurations previously unseen.

Balls of Different Masses

Here, the NPE is trained on worlds with 3, 4, or 5 balls and is tested on unobserved worlds with 6, 7, and 8 balls. From heavest to lightest, cyan, red, and yellow-green colors indicate the different masses. Note that the NPE faithfully predicts transfer of momentum between objects of different mass, and this knowledge of mass is preserved in the test worlds.

Train: worlds with fewer balls

3 Balls of Different Mass

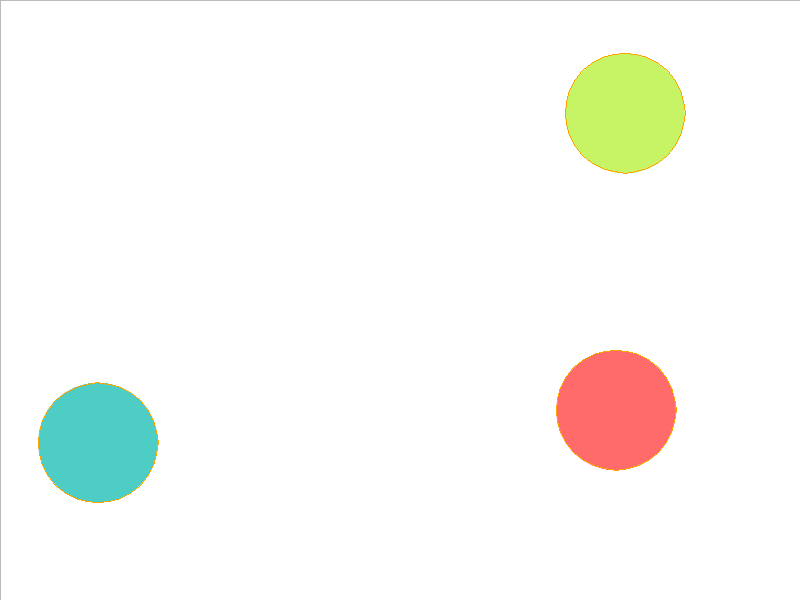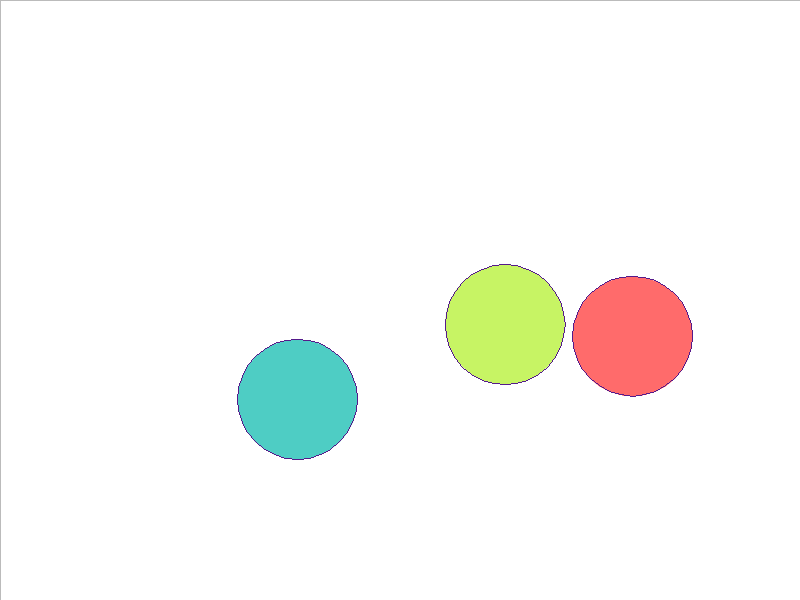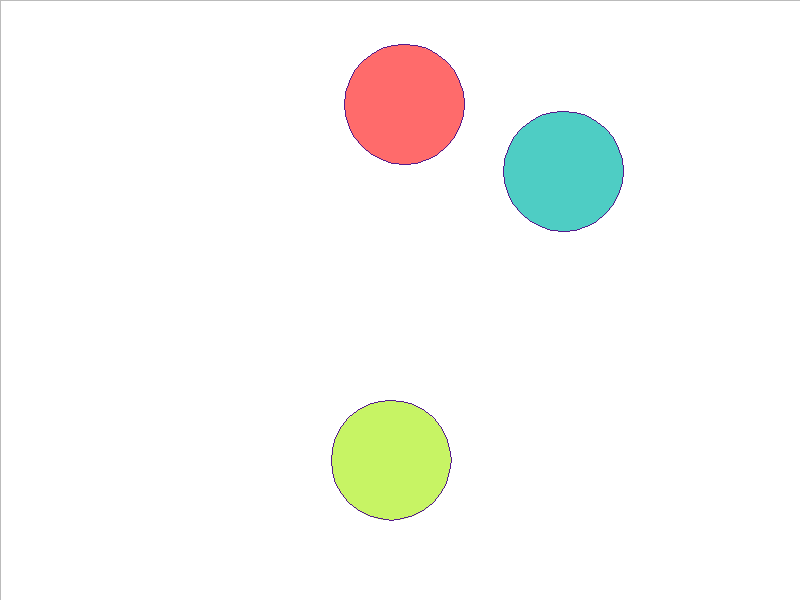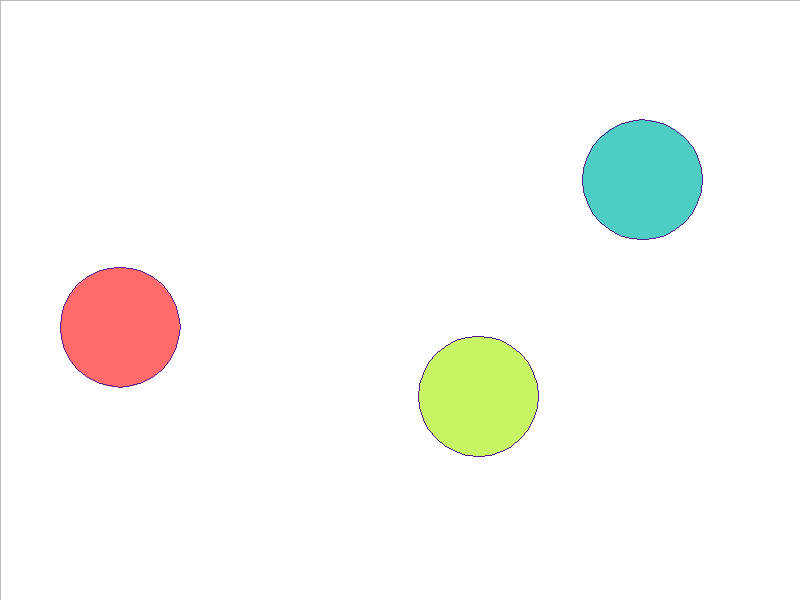Ground Truth NPE Prediction

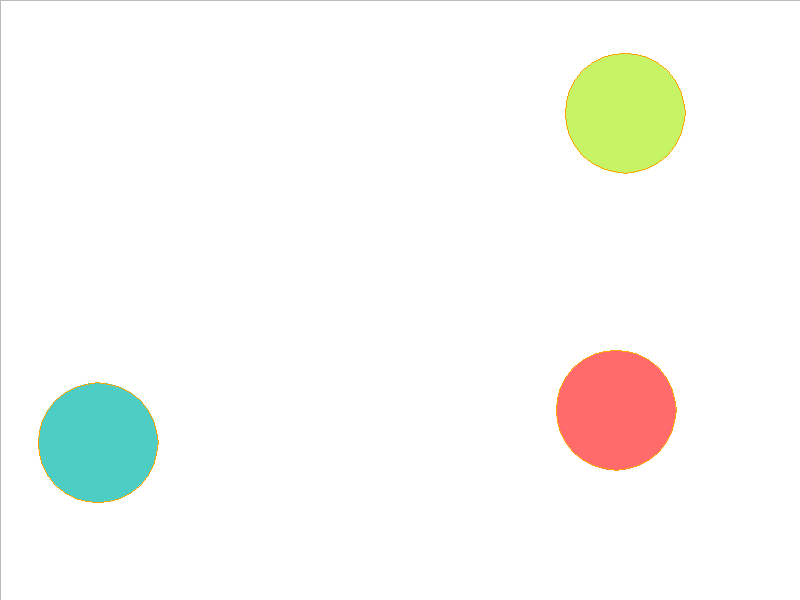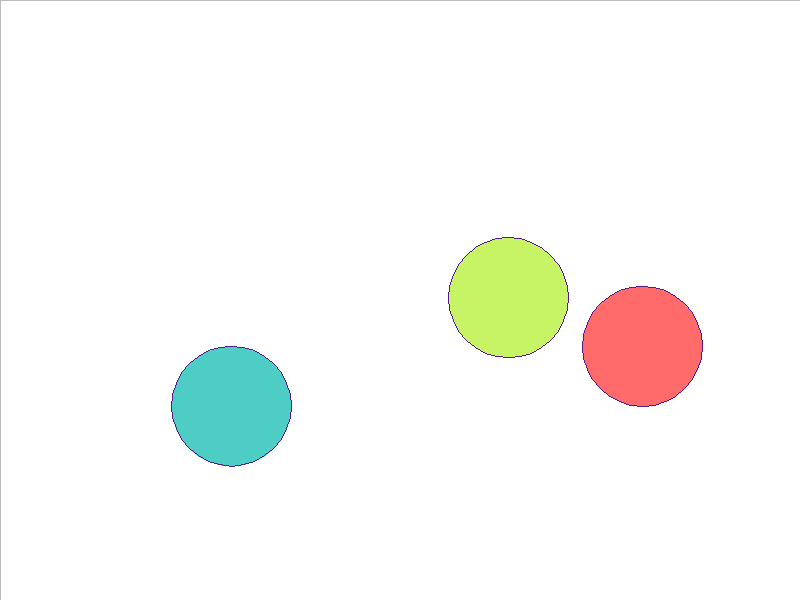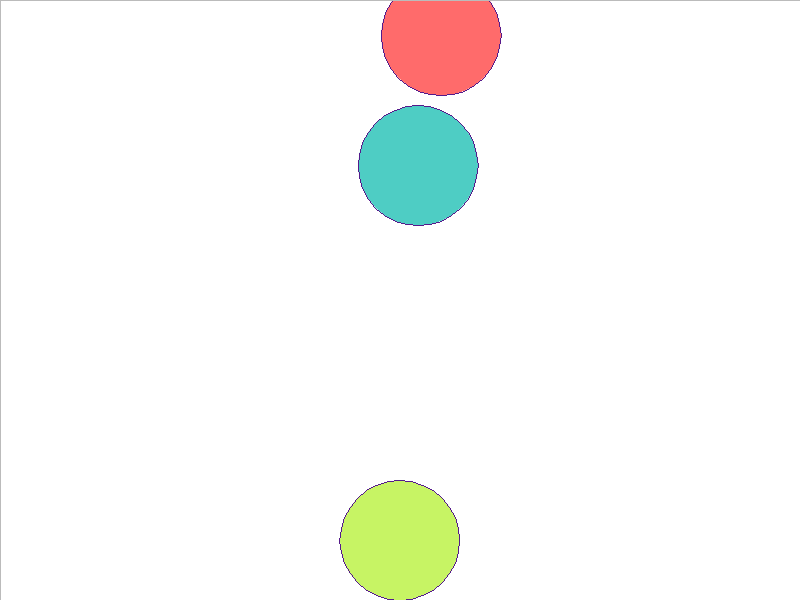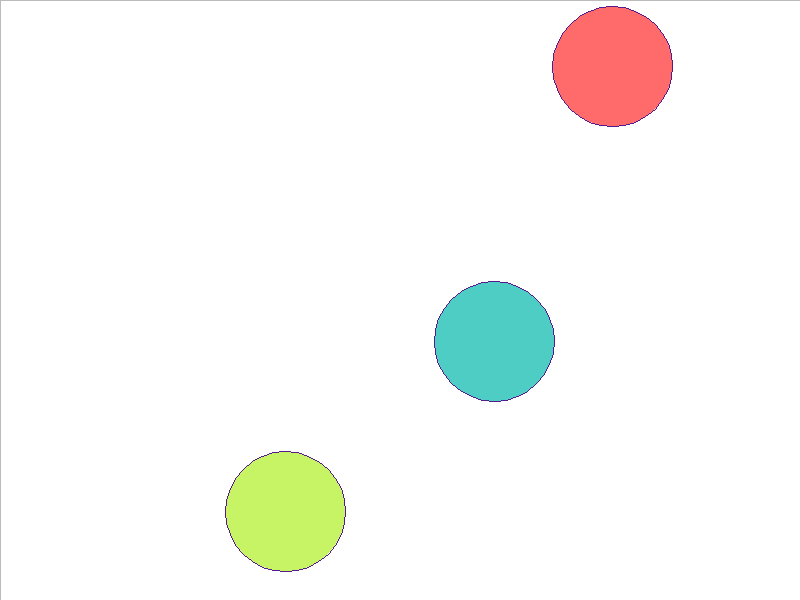
4 Balls of Different Mass

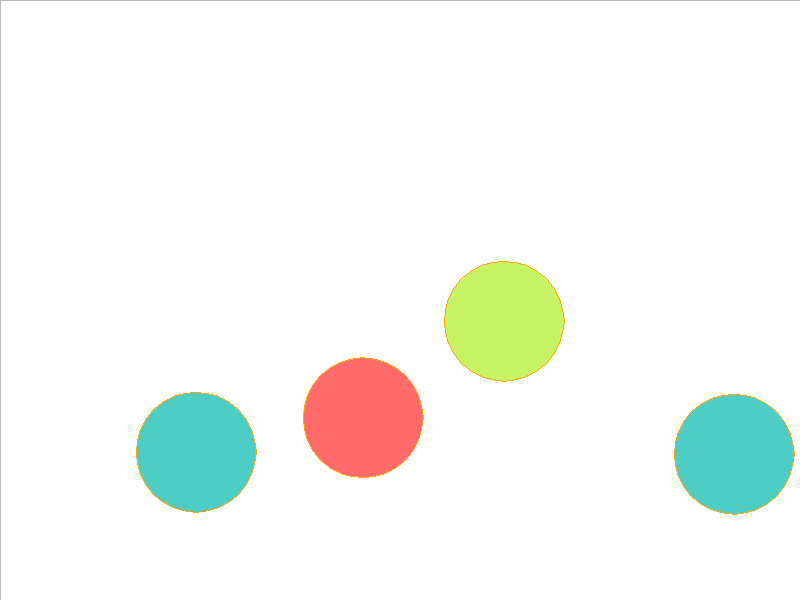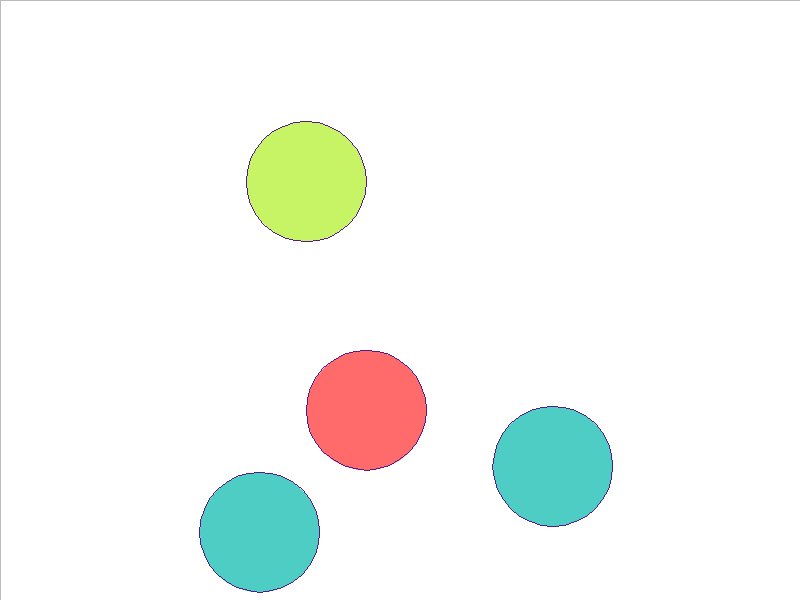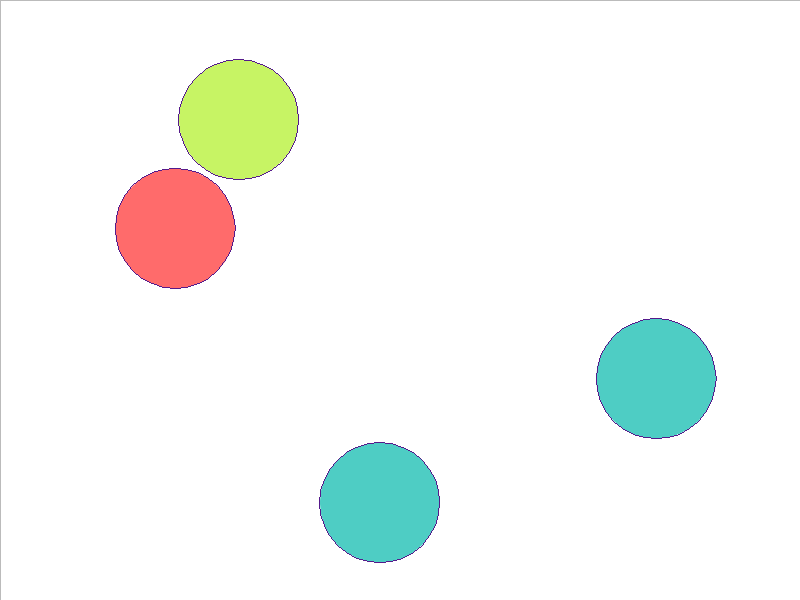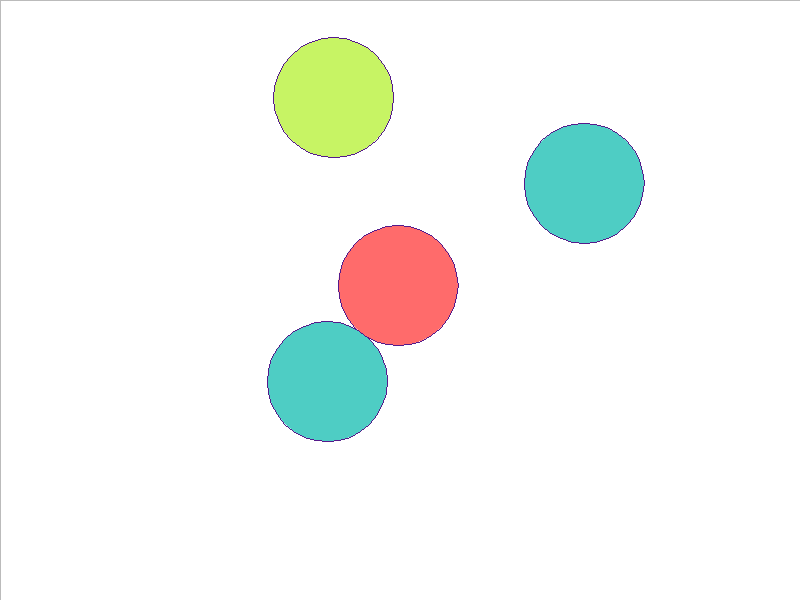Ground Truth NPE Prediction

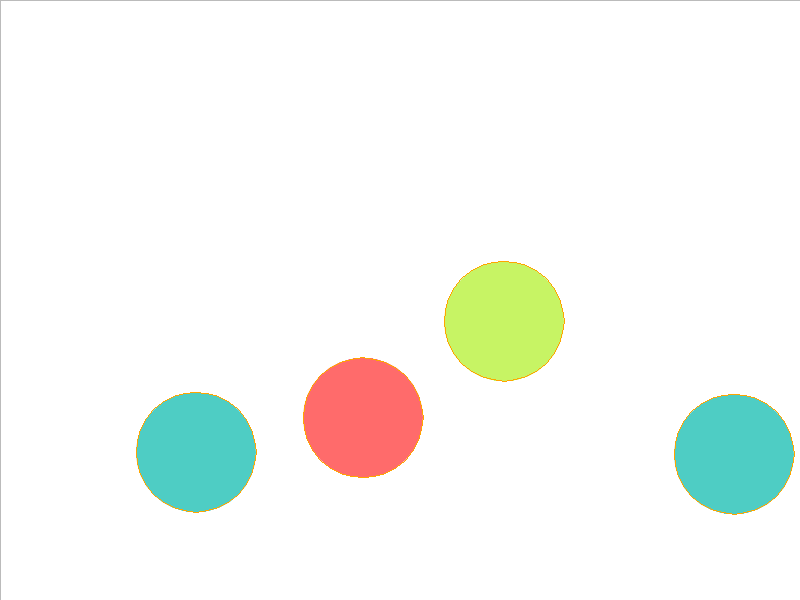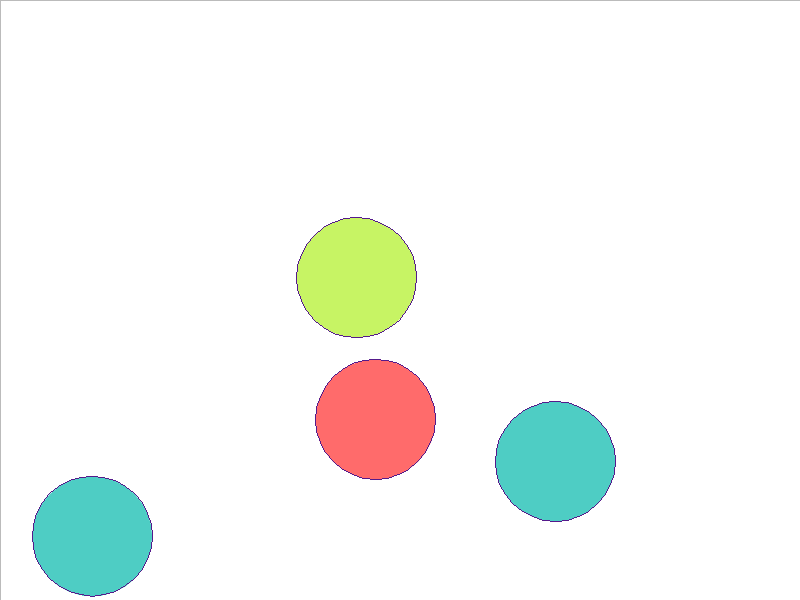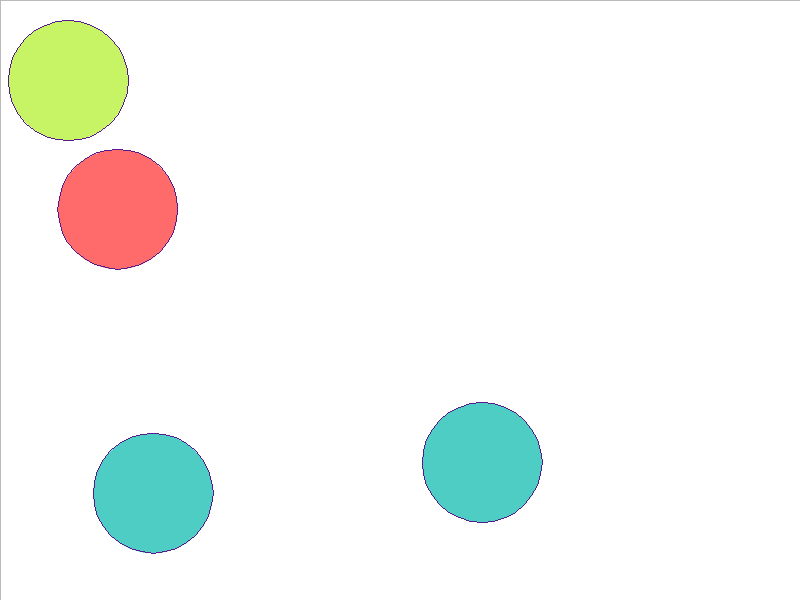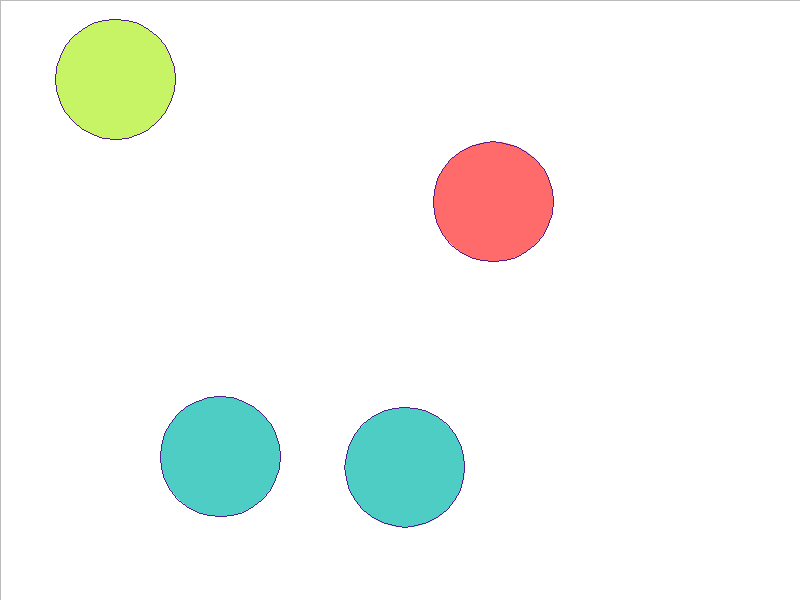
5 Balls of Different Mass

Ground Truth NPE Prediction

Test: worlds with more balls

6 Balls of Different Mass

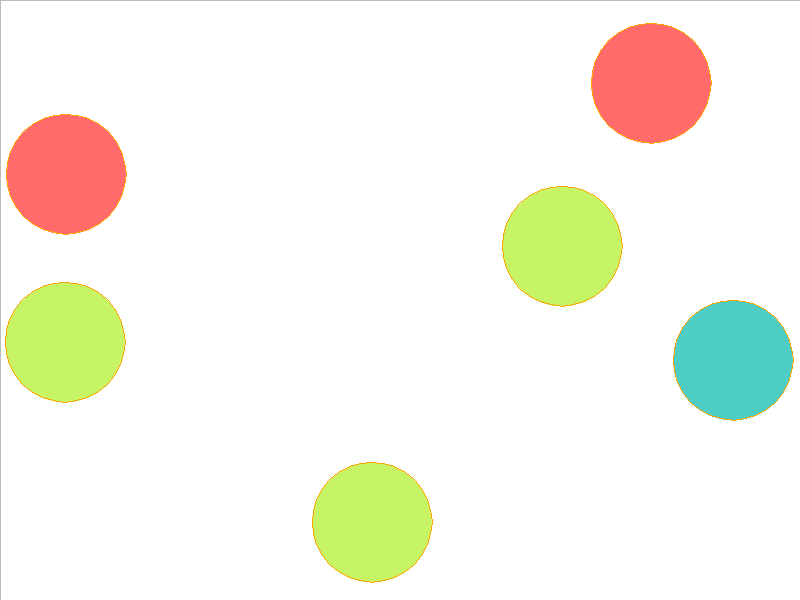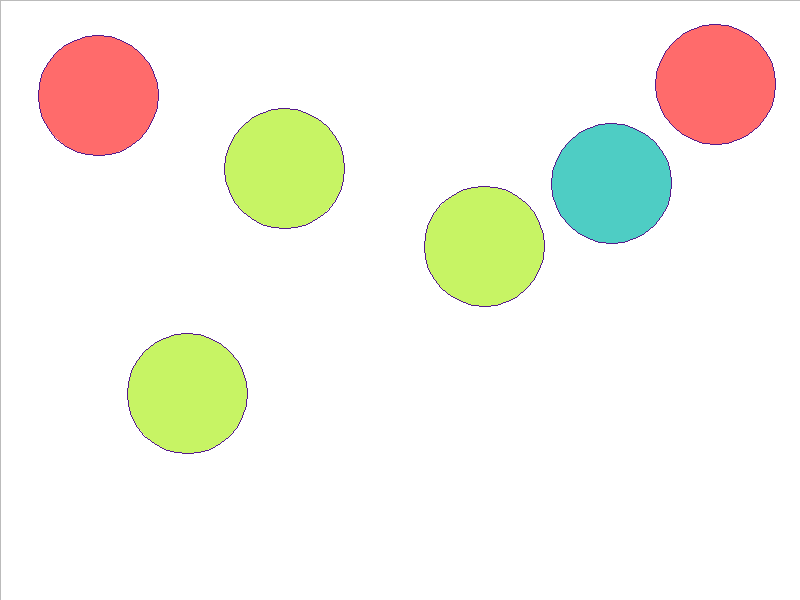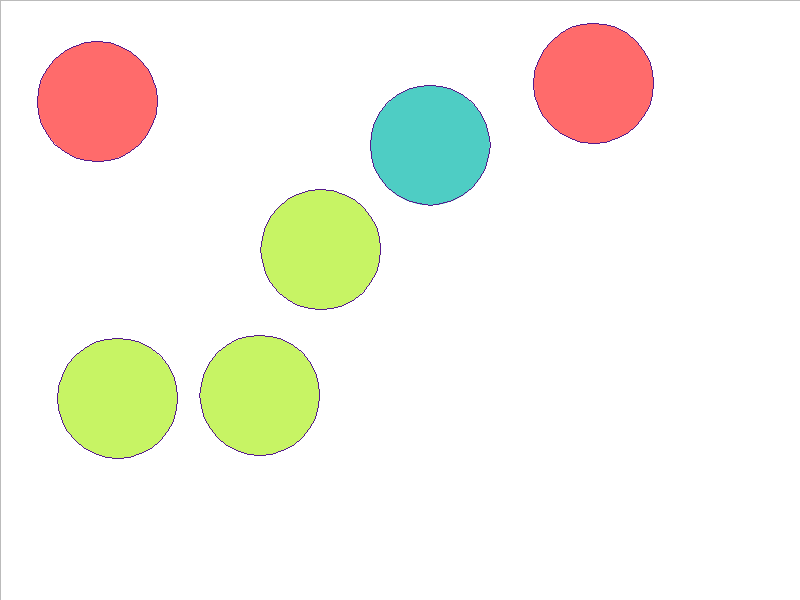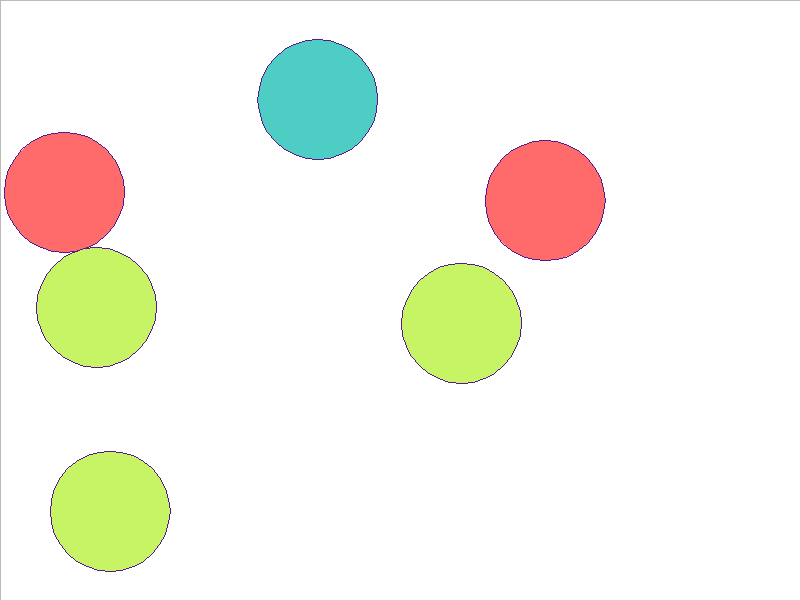Ground Truth NPE Prediction

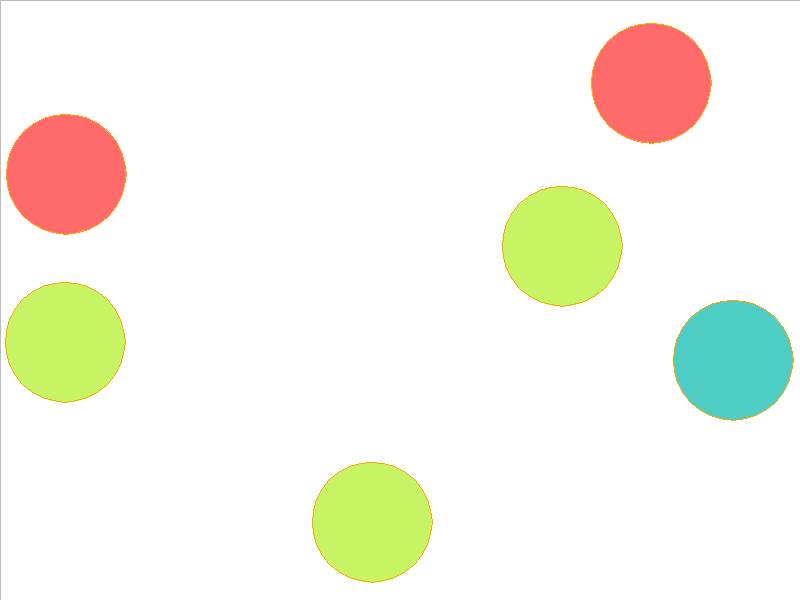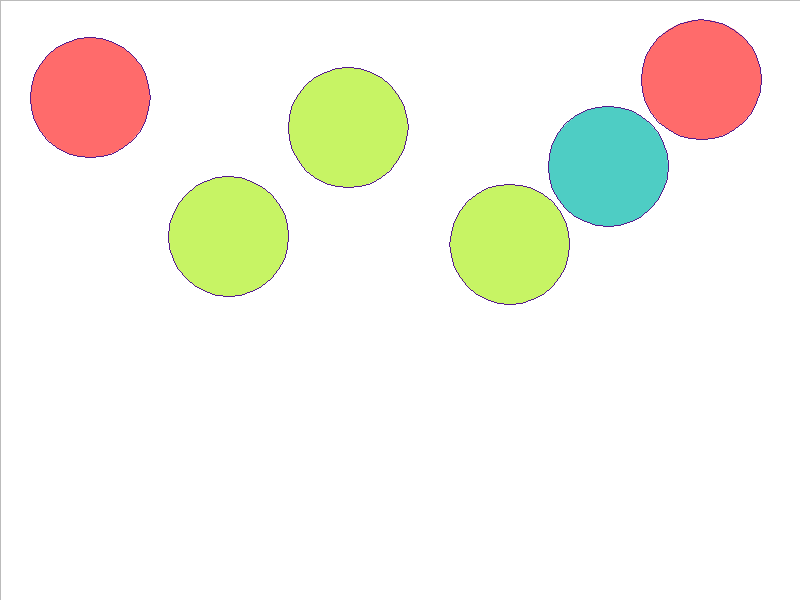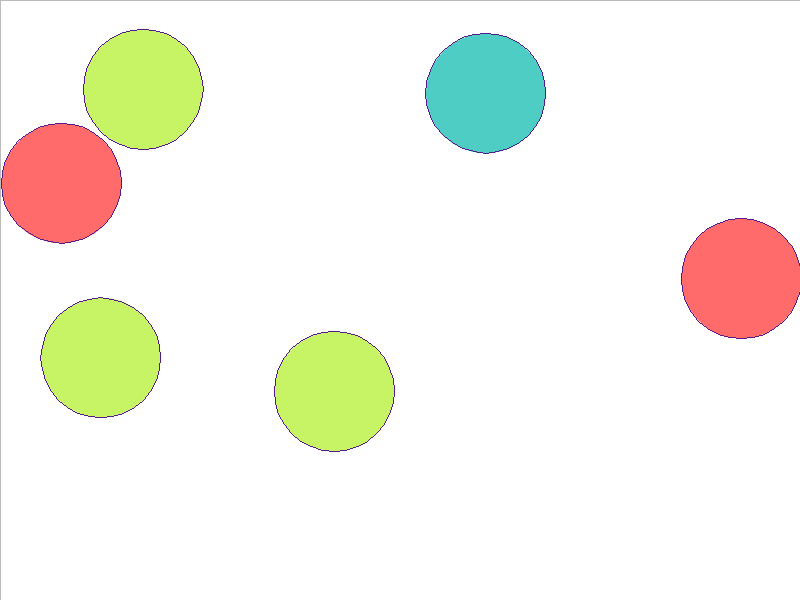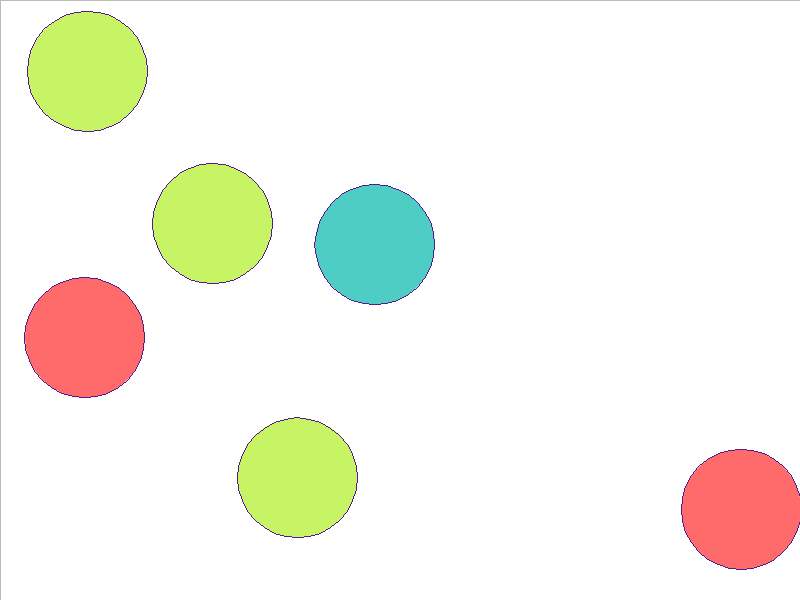
7 Balls of Different Mass

Ground Truth NPE Prediction

8 Balls of Different Mass

Ground Truth NPE Prediction

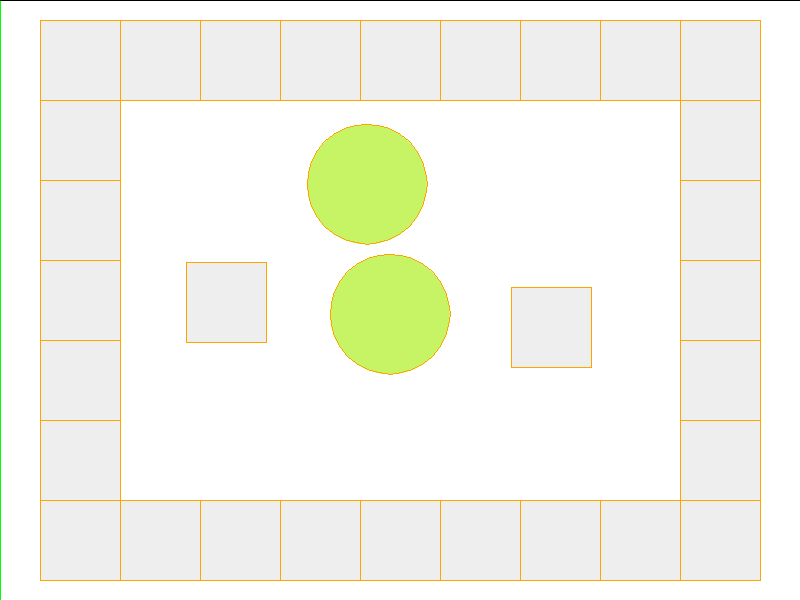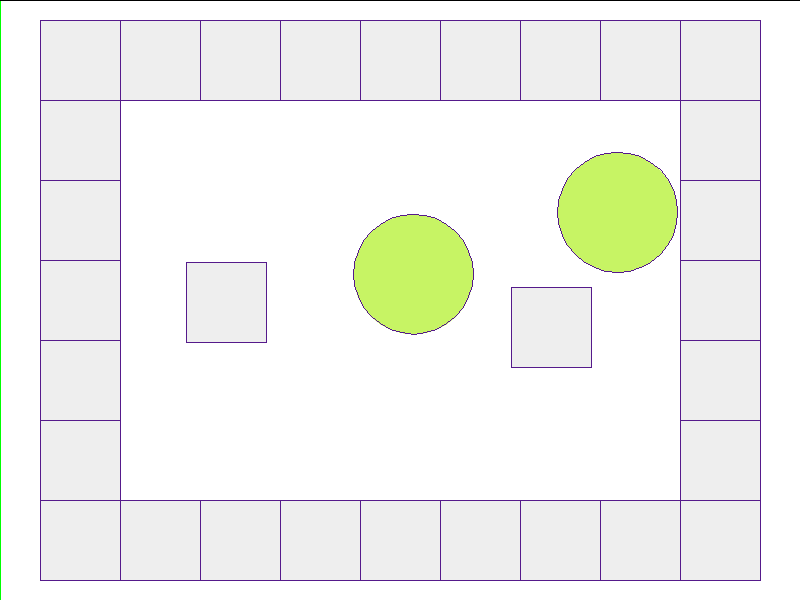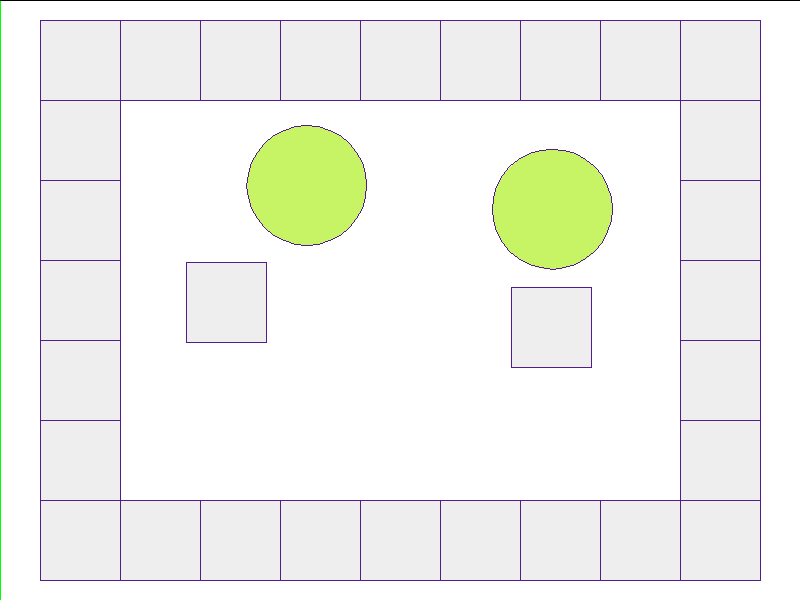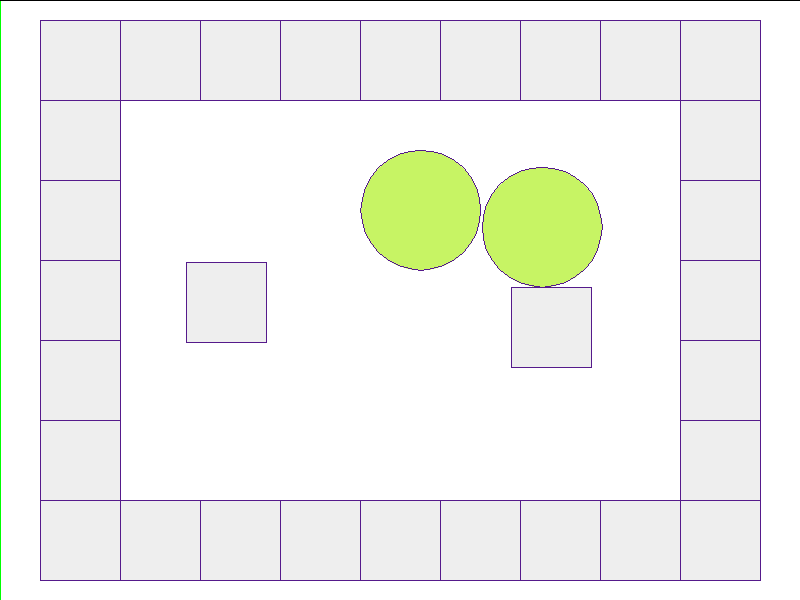
Walls and Obstacles

Here, the NPE is trained on worlds with no internal obstacles and is tested on unobserved worlds with internal obstacles. Variations in wall geometries add to the difficulty of this extrapolation task. Our state space representation formualtes macro-structures such as walls to be composed of smaller building-blocks. Therefore, by this design, the NPE scales to worlds with complex configurations.

Train: worlds without internal obstacles

Ground Truth NPE Prediction

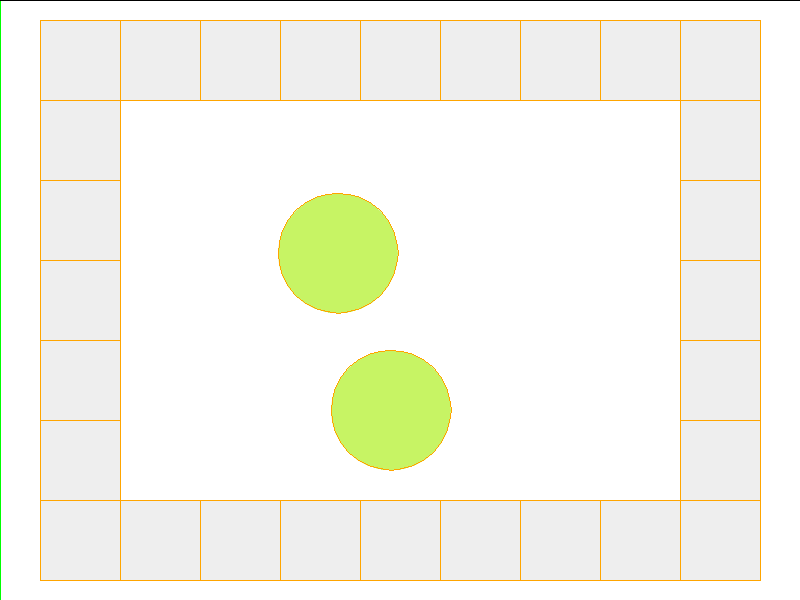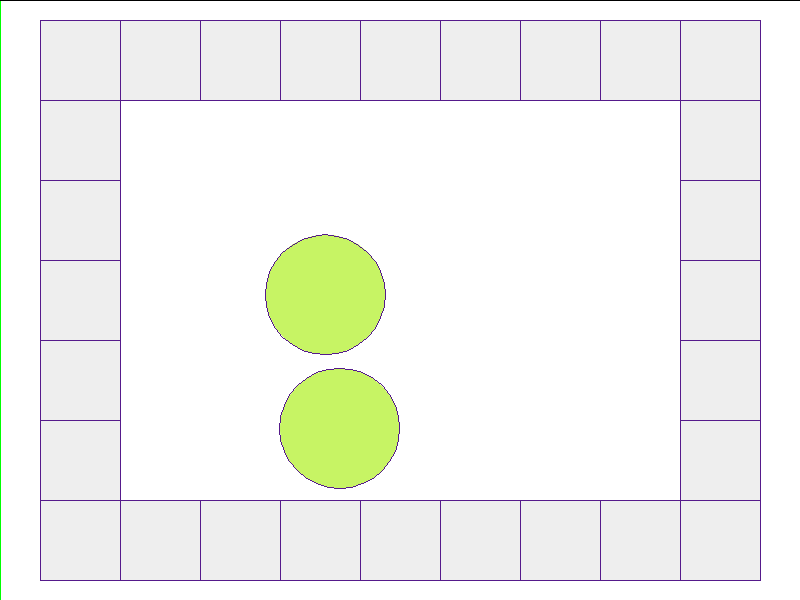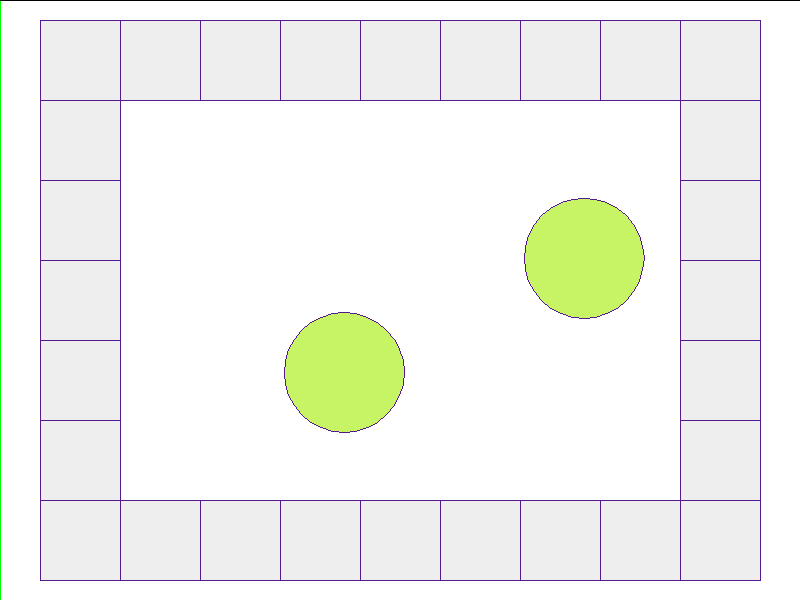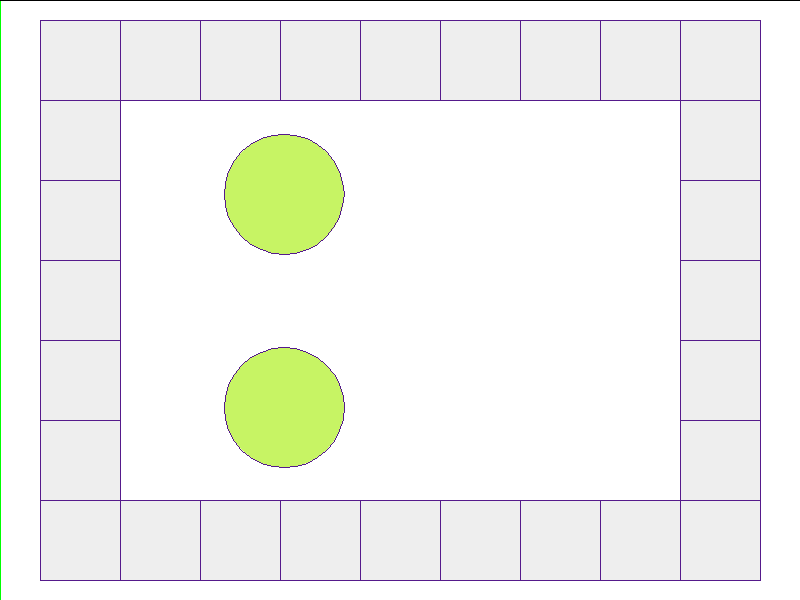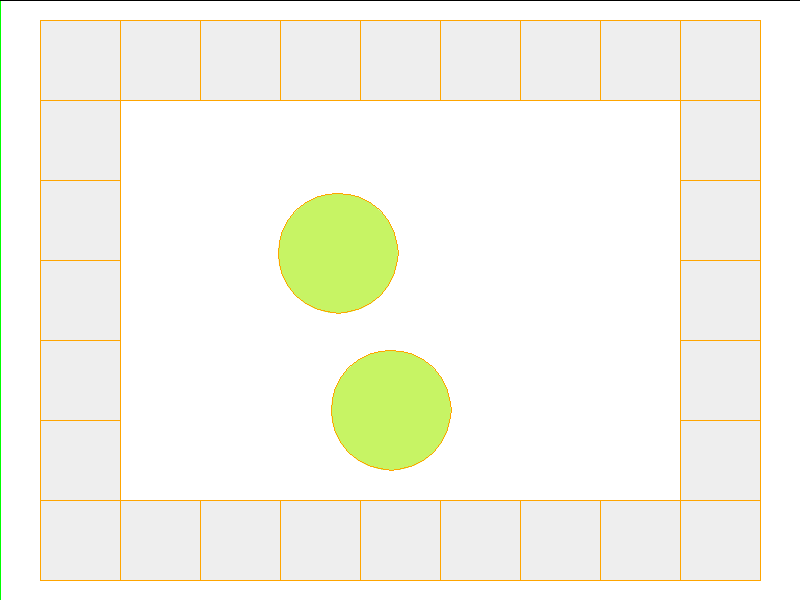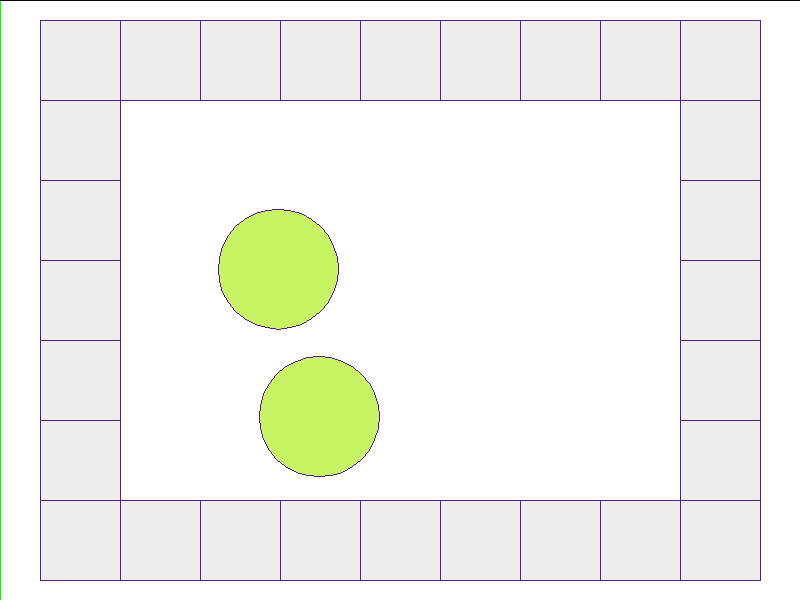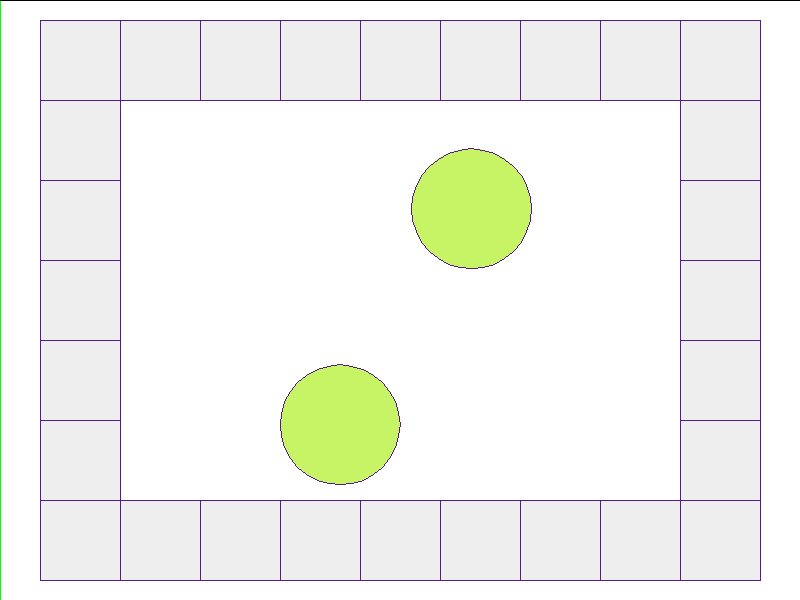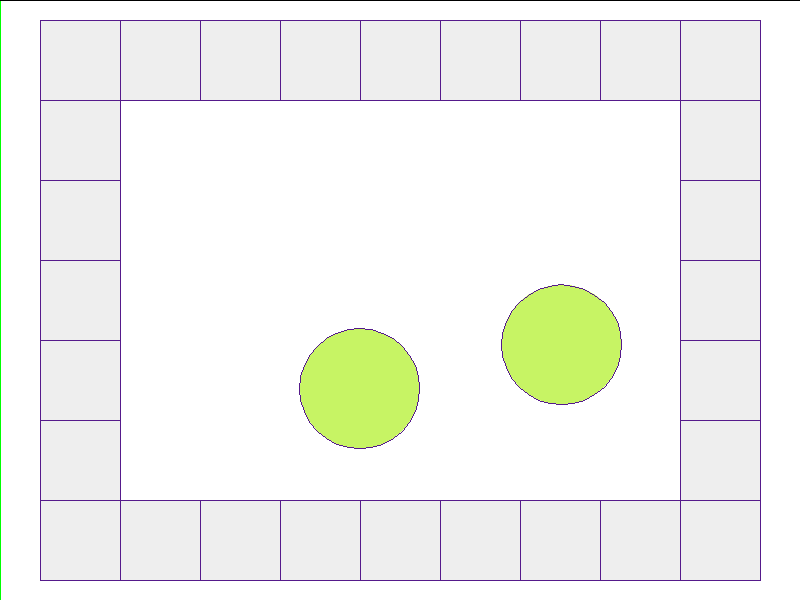
Ground Truth 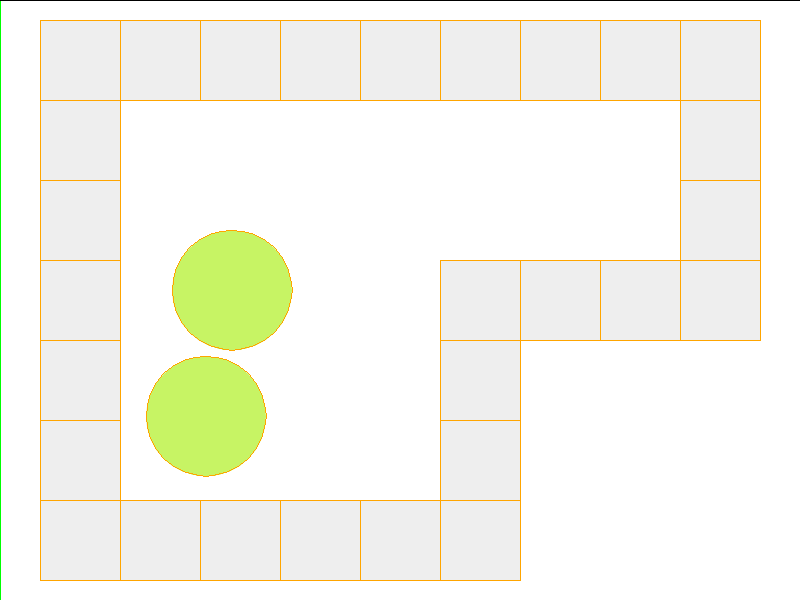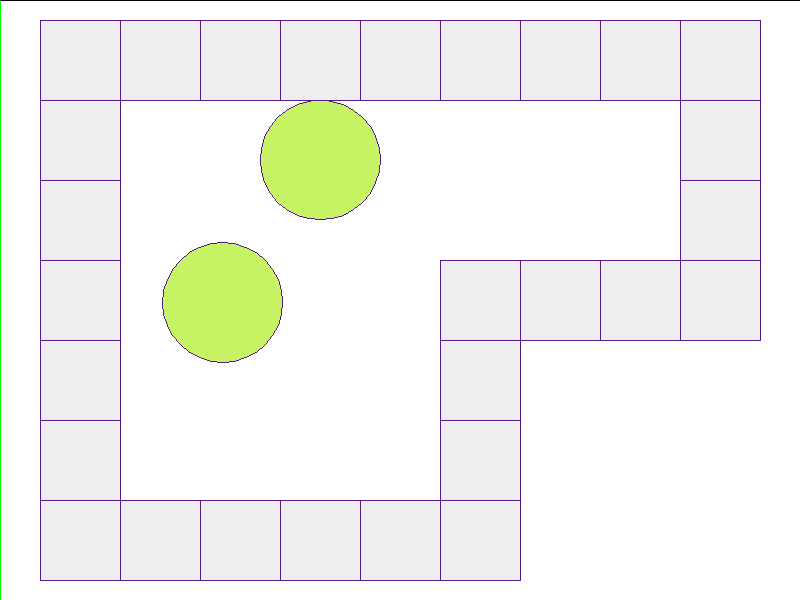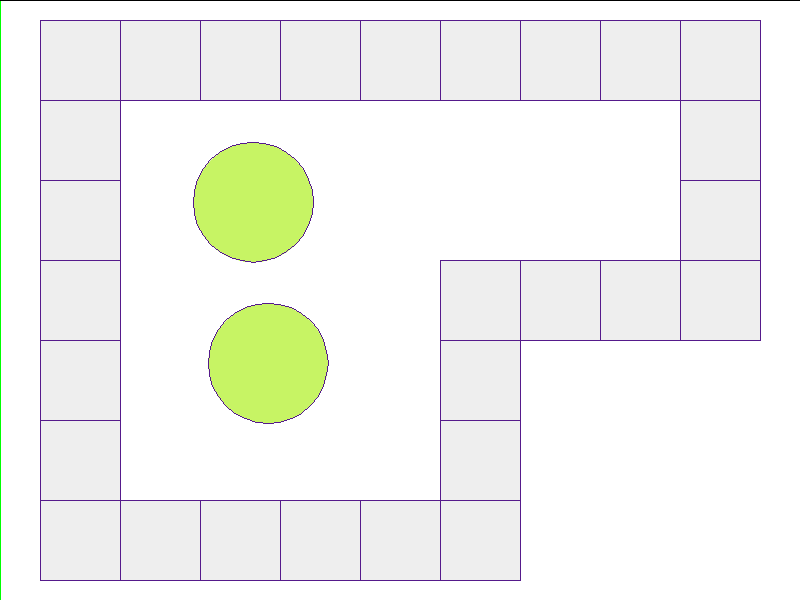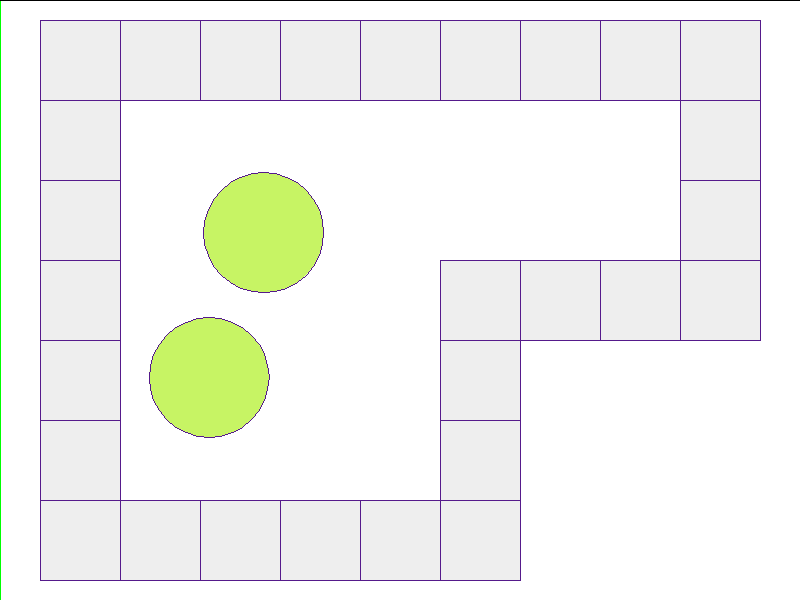NPE Prediction

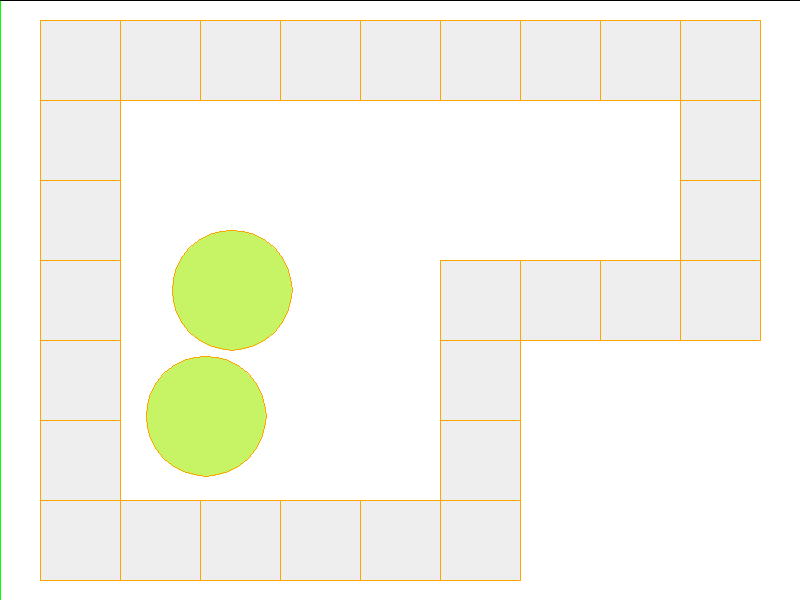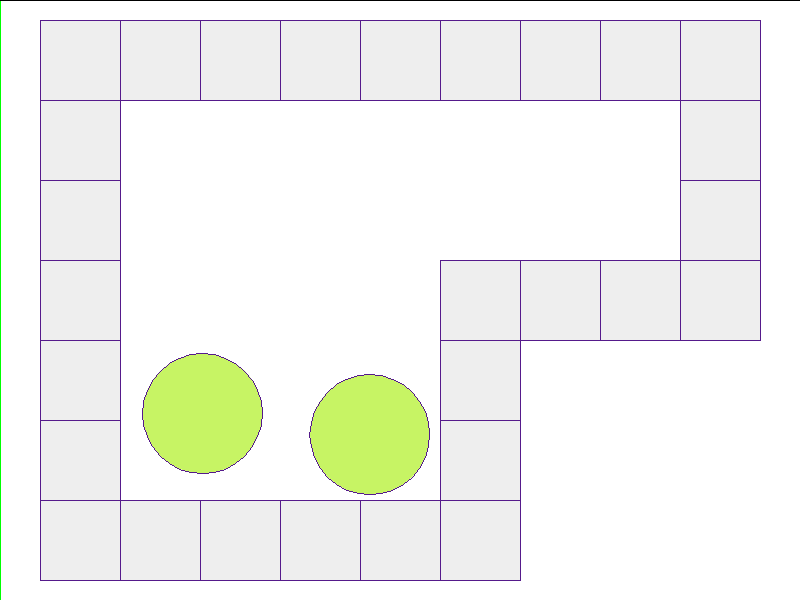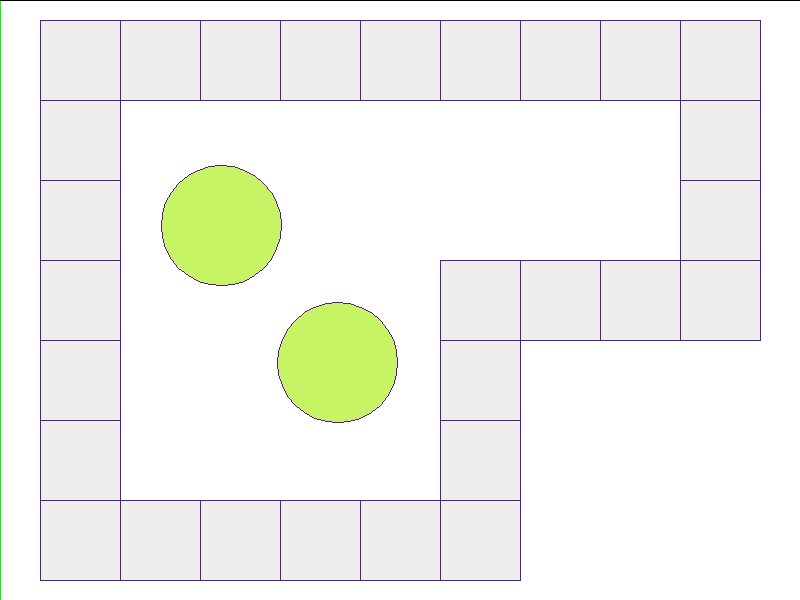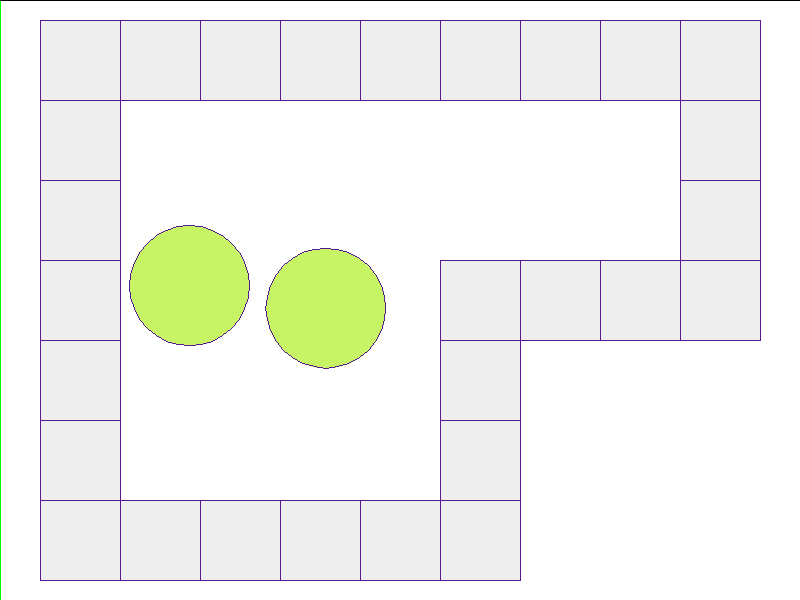
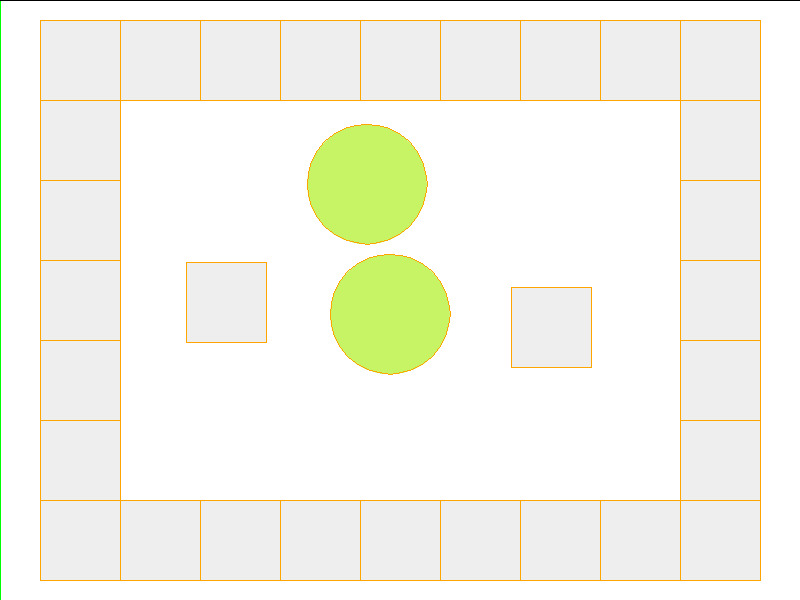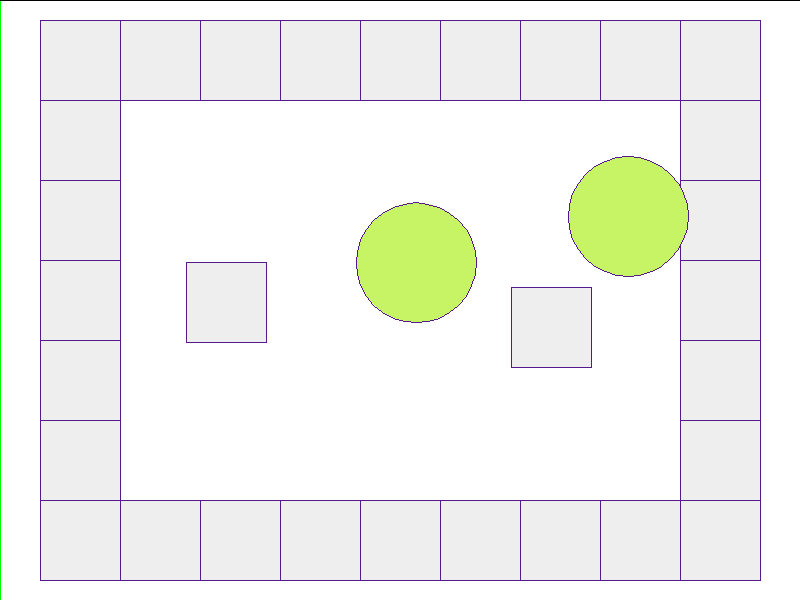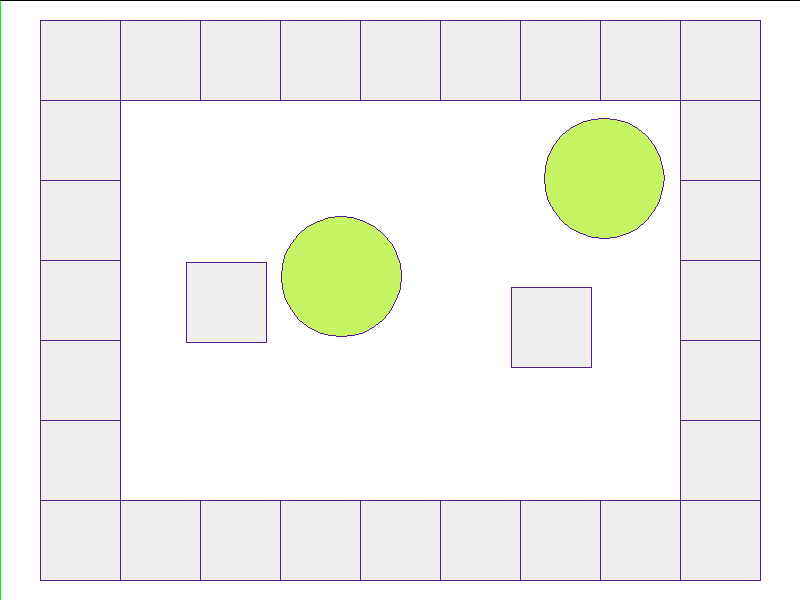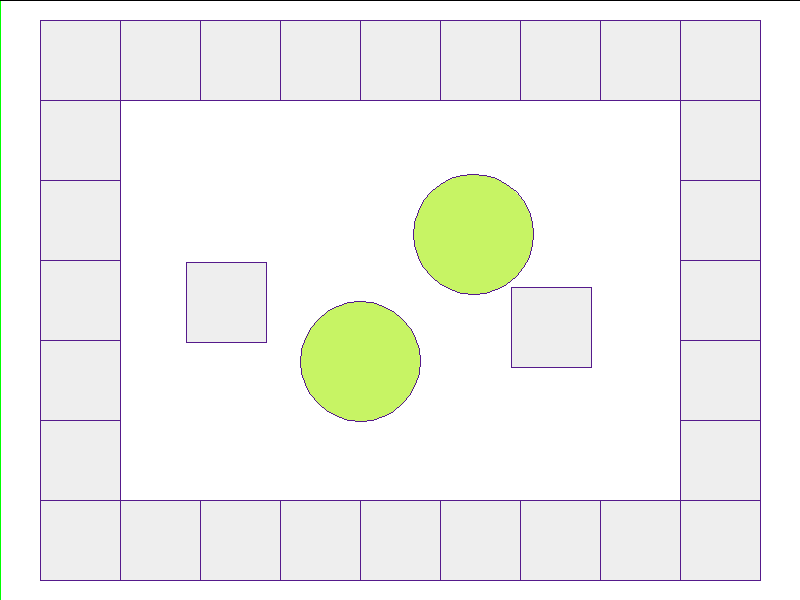
Test: worlds with internal obstacles

Ground Truth NPE Prediction

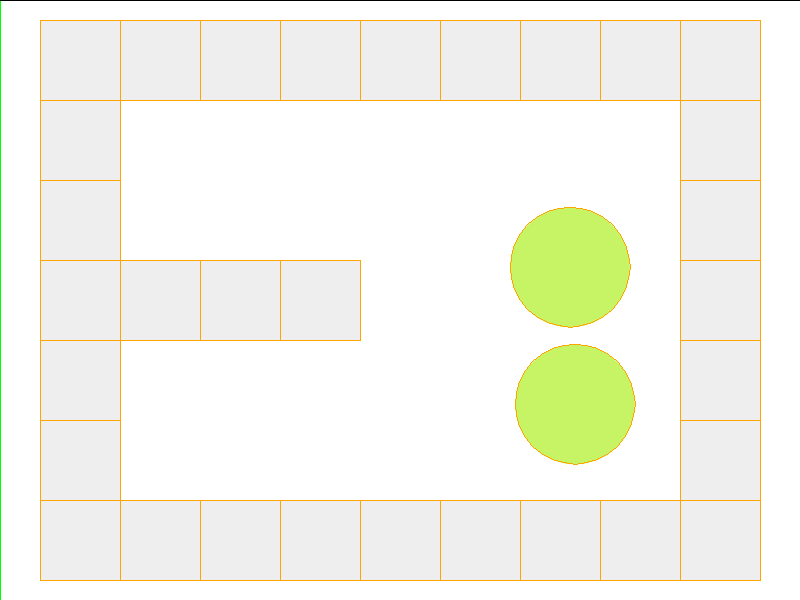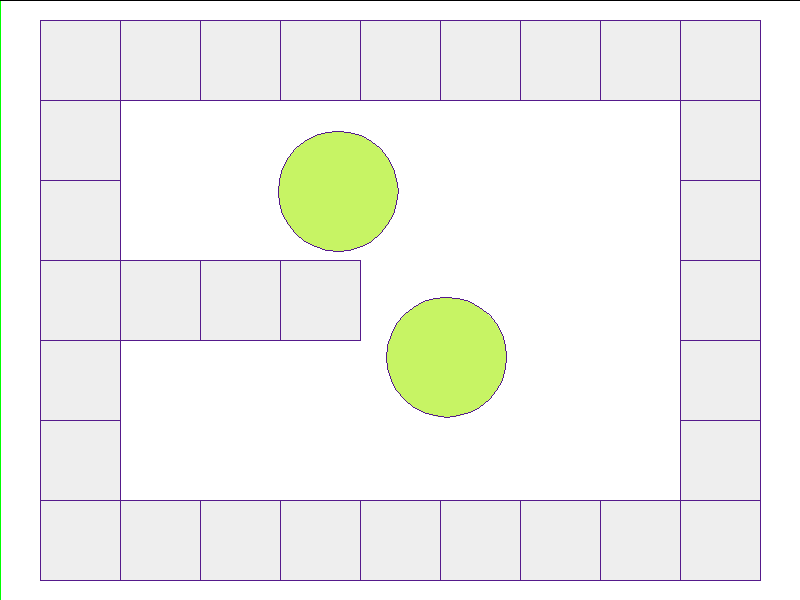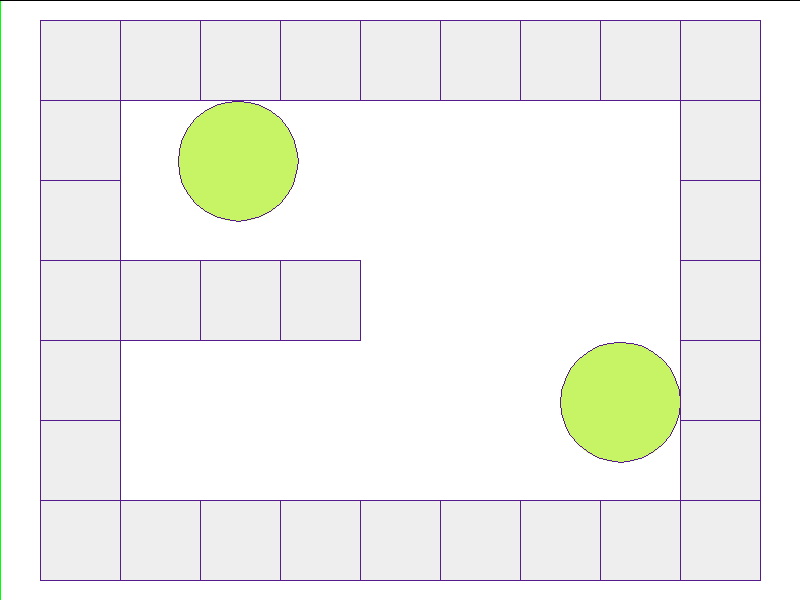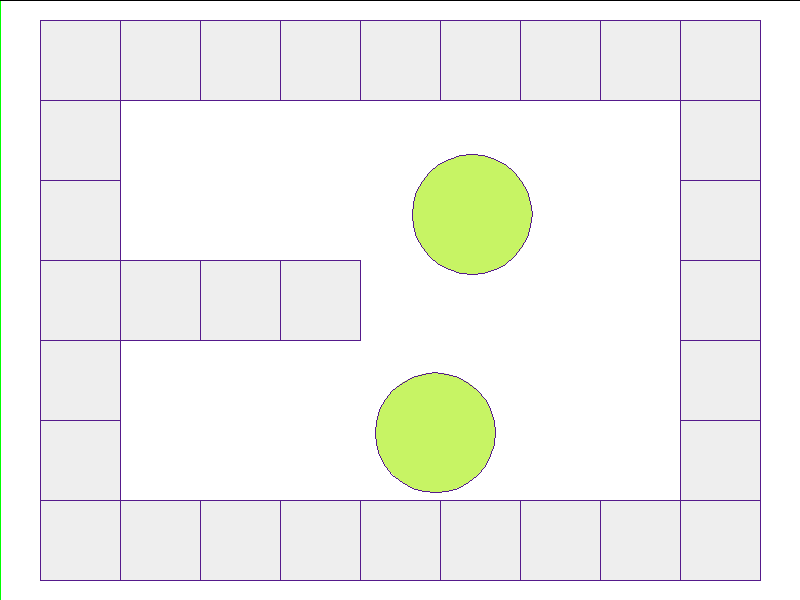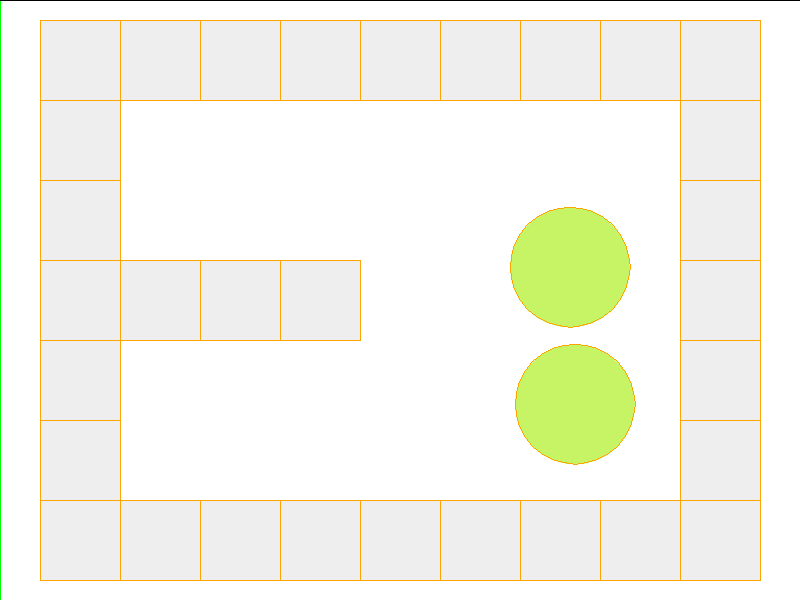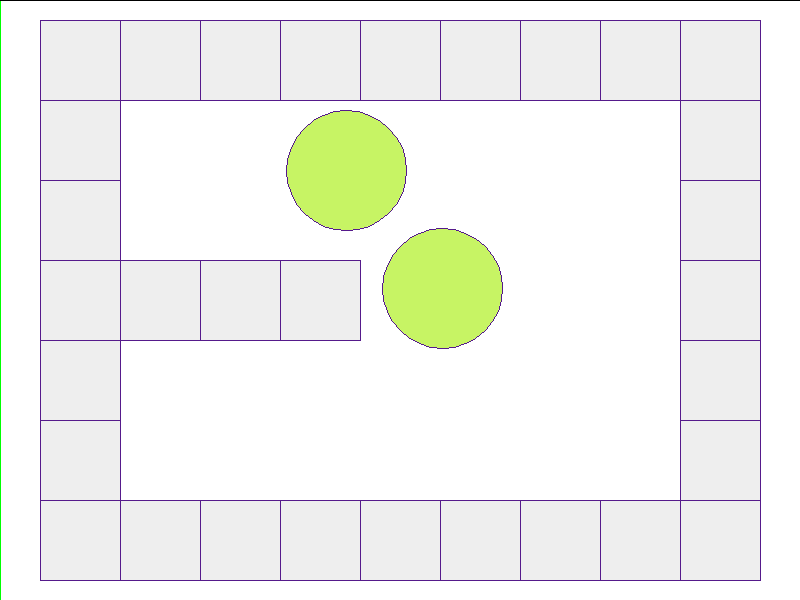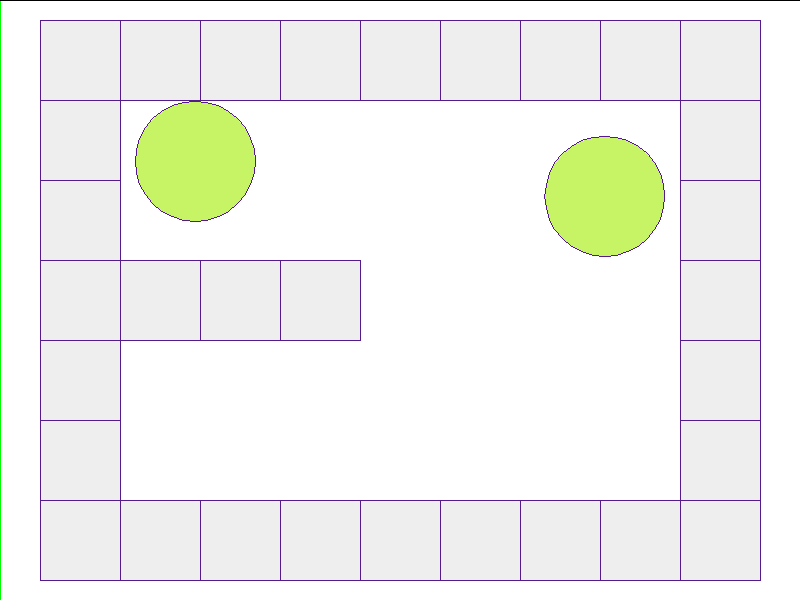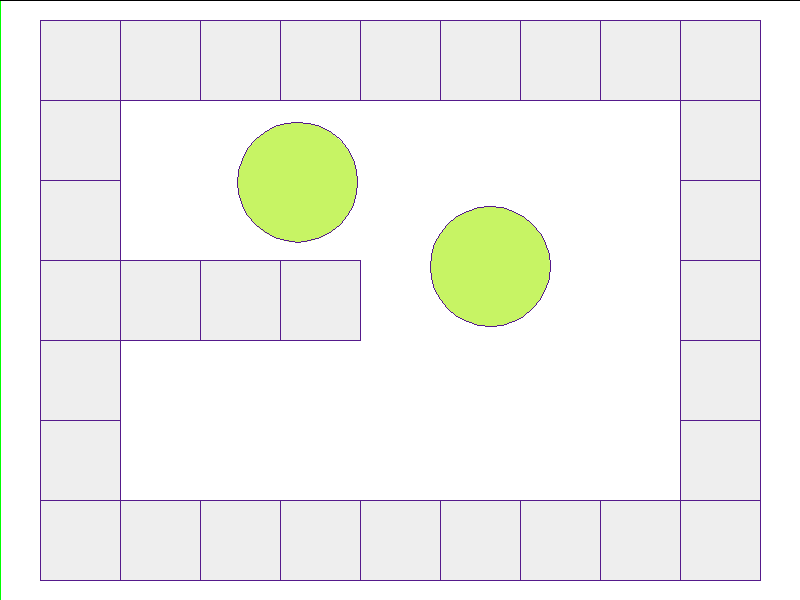
Ground Truth NPE Prediction

Code

Citation

If this paper was helpful, or if you use our code, please cite us!

@article{chang2016compositional,
    title={A Compositional Object-Based Approach to Learning Physical Dynamics},
    author={Chang, Michael B and Ullman, Tomer and Torralba, Antonio and Tenenbaum, Joshua B},
    journal={arXiv preprint arXiv:1612.00341},
    year={2016}
}